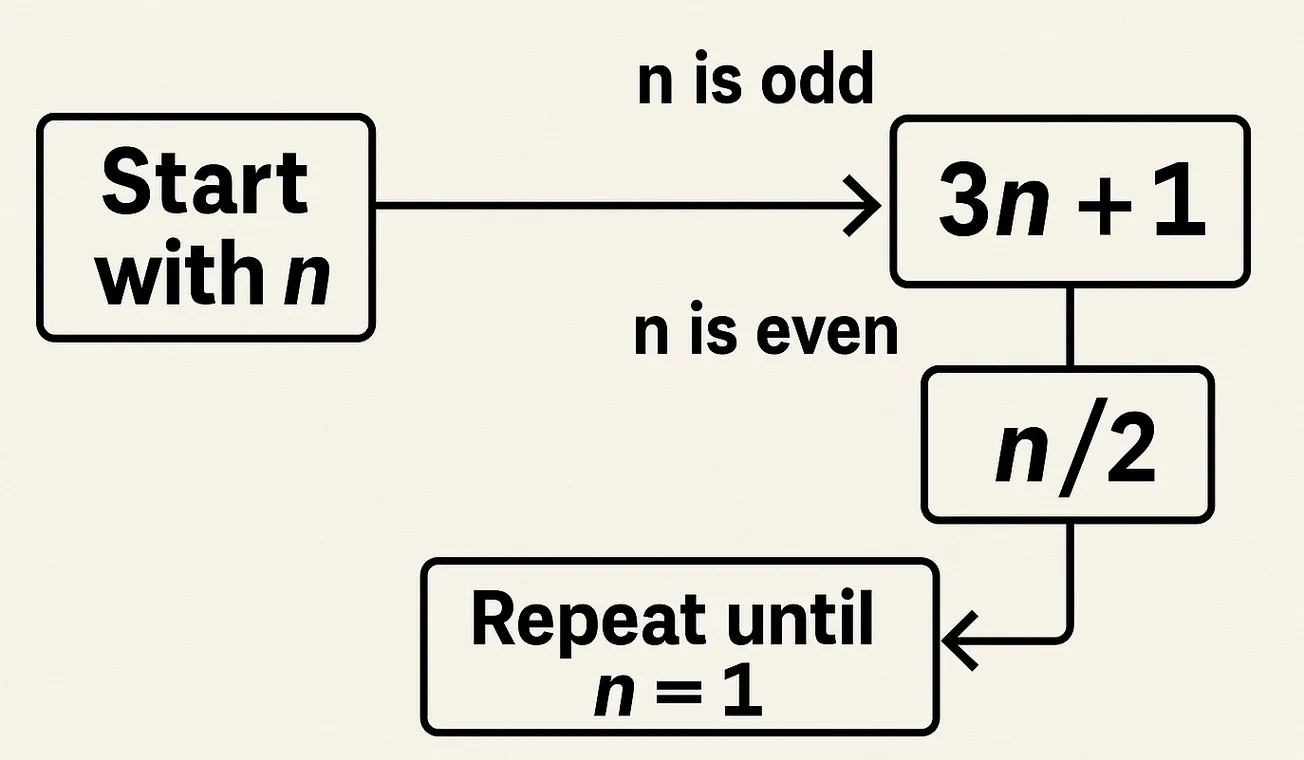
The Collatz conjecture (also known as the 3n+1 problem) is deceptively simple: Start with any positive integer n. If n is even, divide it by 2; if odd, multiply by 3 and add 1. Repeat this process, and the conjecture claims you'll always eventually reach 1 (and then cycle through 4 → 2 → 1). It has been empirically verified for enormous numbers (up to about 2.36 × 10²¹ as of recent checks), but no one has proven it holds for every positive integer. Below, I'll explain why it's so hard, based on insights from mathematical sources like Quanta Magazine, Wikipedia, and expert discussions (e.g., from Terence Tao, Jeffrey Lagarias, and others). I'll also highlight where the core difficulty is "hidden."
1. The Core Mathematical Challenges
- Unpredictable and Chaotic Sequence Behavior:
- The sequence can fluctuate wildly—sometimes increasing dramatically (e.g., via the 3n+1 step) before decreasing (via divisions by 2). For example, after an odd n, you get 3n+1 (even), then divide by 2 to get (3n+1)/2. This result could be even (leading to more divisions and a quick drop) or odd (leading to another potential increase). This unpredictability makes it impossible to guarantee a consistent "downward trend" toward 1 for all starting points.
- Unlike simpler variants (e.g., a "Nollatz" version where odd steps just add 1, which can be proven to decrease), the Collatz rule mixes multiplication by 3 with divisions by 2 in ways that defy easy pattern prediction. Attempts to prove a net decrease fail because the sequence can temporarily "explode" upward before collapsing.
- Infinite Domain and the Risk of Rare Exceptions:
- The conjecture must hold for all infinitely many positive integers. Even if it works for trillions of numbers, a single counterexample (a sequence that diverges to infinity or enters a cycle not involving 1) would disprove it. No such counterexample has been found, but history shows similar conjectures (e.g., Pólya's or Mertens') were disproven by rare, huge exceptions.
- Probabilistic heuristics suggest sequences decrease "on average" (e.g., there's a 50% chance the next term after an odd step is even, leading to more divisions), but this doesn't rule out outliers. Experts like Riho Terras (1976) and Terence Tao (2019) have proven that "almost all" numbers eventually drop below their starting point (or even much lower, like below √n), but "almost all" isn't "all." Tao called his result "as close as we can get without solving it," underscoring the gap.
- Difficulty in Ruling Out Cycles or Divergence:
- A key fear is hidden cycles: sequences that loop without reaching 1 (e.g., something like 5 → 16 → 8 → 4 → 2 → 1 is fine, but a non-trivial loop like hypothetical 7 → 22 → 11 → 34 → 17 → 52 → 26 → 13 → 40 → 20 → 10 → 5 → ... wait, that's not a loop). Searches have ruled out small cycles (up to length 91) and set huge lower bounds on possible cycle lengths (e.g., over 10¹¹), but proving no cycles exist at all is elusive.
- Divergence (growing forever) is also hard to disprove rigorously, as the sequence's growth isn't bounded in a provable way.
2. Where the Difficulty is Hidden
- The 'Hidden' Issue: Lack of Structure for Standard Proof Techniques:
- The conjecture sits at the intersection of number theory, dynamics, and chaos, but it doesn't fit neatly into tools like modular arithmetic, Diophantine equations, or ergodic theory. It involves operations modulo powers of 2 (divisions) mixed with linear growth (3n+1), creating a "mixing" effect that's hard to analyze globally. As Lagarias put it, it's "out of reach of present-day mathematics"—we lack the framework to handle its blend of simplicity and irregularity.
- It's "treacherously alluring" because it's easy to state and test but resists induction, contradiction, or invariant-based proofs. For instance, reverse-engineering (working backward from 1) branches exponentially, creating an infinite tree that's hard to fully explore.
- Connections to deeper mysteries: Some see ties to prime numbers' unpredictability or even undecidability. Generalizations of Collatz are provably undecidable (per John Conway), and the problem is Π⁰₂-complete in certain forms, hinting it might be inherently unprovable in standard axioms (like Peano arithmetic), though this isn't confirmed for the original.
- Empirical Success vs. Proof Failure:
- The difficulty is "hidden" in the illusion of simplicity—computers confirm it for vast ranges, lulling us into thinking it's obvious, but scaling to infinity exposes gaps. Heuristics and partial proofs (e.g., Tao's) tease progress but stall at universality.
3. Why It's Not Proven (Failed Approaches and Expert Views)
- Failed Approaches:
- Empirical Verification: Checking billions of numbers isn't a proof; it misses potential huge counterexamples.
- Heuristics and Averages: Statistical models predict convergence but aren't rigorous for all cases.
- Cycle Hunting: Algorithms detect no cycles in tested ranges, but exhaustive search is impossible for infinity.
- Partial Proofs: Results like Tao's cover "almost all" but leave room for exceptions.
- Expert Insights:
- Terence Tao: Emphasizes the challenge in bridging "almost all" to "all," noting the conjecture's "dangerous" allure due to its simplicity hiding deep chaos.
- Jeffrey Lagarias: Calls it an "extraordinarily difficult problem" that's "not at all amenable to solution."
- Paul Erdős: Famously said, "Mathematics may not be ready for such problems," capturing its elusive nature.
- Community Views (e.g., Reddit, Stack Exchange): Often link it to primes' mysteries or note its value lies in the unsolved pursuit, not the result.
In summary, the difficulty is hidden in the conjecture's chaotic, unpredictable dynamics over an infinite set, where rare behaviors (cycles, divergence) can't be fully ruled out with current tools. It's a problem that seems "solved" computationally but exposes the limits of mathematical proof. If proven, it might require breakthroughs in understanding integer dynamics; if disproven, a massive counterexample. For now, it remains one of math's most tantalizing open questions.